GONIOMETRIA

Circonferenza goniometrica

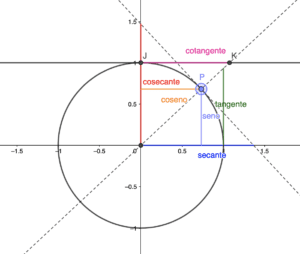
$\displaystyle \sin (\theta) = y_p$

$\displaystyle \cos (\theta) = x_p$

$\displaystyle \tan (\theta) = \frac{\sin (\theta) }{\cos (\theta)}$

$\displaystyle \sec(\theta) = \frac{1 }{\cos (\theta)}$

$\displaystyle \csc(\theta) = \frac{1 }{\sin(\theta)}$

$\displaystyle \cot(\theta) = \frac{1 }{\tan(\theta)}$

Angoli particolari

$\displaystyle \sin 0 = 0, \quad \cos 0 = 1, \quad \tan 0 = 0$

$\displaystyle \sin 30 = \frac{1}{2}, \quad \cos 30 = \frac{\sqrt{3}}{2}, \quad \tan 30 = \frac{1}{\sqrt{3}}$

$\displaystyle \sin 45 = \frac{\sqrt{2}}{2}, \quad \cos 45 = \frac{\sqrt{2}}{2}, \quad \tan 45 = 1$

$\displaystyle \sin 60 = \frac{\sqrt{3}}{2}, \quad \cos 60 = \frac{1}{2}, \quad \tan 60 = \sqrt{3}$

$\displaystyle \sin 90 = 1, \quad \cos 90 = 0, \quad \tan 90 \text{ (Non definita)}$

$\displaystyle \sin 180 = 0, \quad \cos 180 = -1, \quad \tan 180 = 0$

$\displaystyle \sin 270 = -1, \quad \cos 270 = 0, \quad \tan 270 \text{ (Non definita)}$

$\displaystyle \sin 360 = 0, \quad \cos 360 = 1, \quad \tan 360 = 0$

Relazione fondamentale della goniometria

$\displaystyle \cos^2(\theta) + \sin^2(\theta) = 1$

$\displaystyle \cos(\theta)=\pm\frac{1}{\sqrt{1+\tan^2(\theta)}} $

$\displaystyle \sin(\theta) =\pm \frac{|\tan(\theta)|}{\sqrt{1+\tan^2(\theta)}} $

Angoli associati

$\displaystyle \sin(-\theta) = -\sin(\theta)$
$\displaystyle \cos(-\theta) = \cos(\theta)$
$\displaystyle \tan(-\theta) = -\tan(\theta)$

$\displaystyle \sin(\pi + \theta) = -\sin(\theta)$
$\displaystyle \cos(\pi + \theta) = -\cos(\theta)$
$\displaystyle \tan(\pi + \theta) = \tan(\theta)$

$\displaystyle \sin(\pi – \theta) = \sin(\theta)$
$\displaystyle \cos(\pi – \theta) = -\cos(\theta)$
$\displaystyle \tan(\pi – \theta) = -\tan(\theta)$

$\displaystyle \sin\left(\frac{\pi}{2} + \theta\right) = \cos(\theta)$
$\displaystyle \cos\left(\frac{\pi}{2} + \theta\right) = \sin(\theta)$
$\displaystyle \tan\left(\frac{\pi}{2} + \theta\right) = \frac{1}{\tan(\theta)}$

$\displaystyle \sin\left(\frac{\pi}{2} – \theta\right) = \cos(\theta)$
$\displaystyle \cos\left(\frac{\pi}{2} – \theta\right) = \sin(\theta)$
$\displaystyle \tan\left(\frac{\pi}{2} – \theta\right) = \frac{1}{\tan(\theta)}$

$\displaystyle \sin\left(\frac{3}{2}\pi + \theta\right) = -\cos(\theta)$
$\displaystyle \cos\left(\frac{3}{2}\pi + \theta\right) = -\sin(\theta)$
$\displaystyle \tan\left(\frac{3}{2}\pi + \theta\right) = \frac{1}{\tan(\theta)}$

$\displaystyle \sin\left(\frac{3}{2}\pi – \theta\right) = \cos(\theta)$
$\displaystyle \cos\left(\frac{3}{2}\pi – \theta\right) = -\sin(\theta)$
$\displaystyle \tan\left(\frac{3}{2}\pi – \theta\right) = -\frac{1}{\tan(\theta)}$

Formule di addizione e sottrazione

$\displaystyle\sin(\alpha + \beta)= \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta)$

$\displaystyle\sin(\alpha – \beta) = \sin(\alpha) \cdot \cos(\beta) – \cos(\alpha) \cdot \sin(\beta)$

$\displaystyle\cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) – \sin(\alpha) \cdot \sin(\beta)$

$\displaystyle\cos(\alpha – \beta) = \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta)$

$\displaystyle\tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 – \tan(\alpha) \cdot \tan(\beta)}$

$\displaystyle\tan(\alpha – \beta) = \frac{\tan(\alpha) – \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)}$

Formule di duplicazione

$\displaystyle \sin(2\alpha) = 2\sin(\alpha)\cos(\alpha)$

$\displaystyle \cos(2\alpha) =  \cos^2(\alpha) – \sin^2(\alpha)$

$\displaystyle \tan(2\alpha) = \frac{2\tan(\alpha)}{1 – \tan^2(\alpha)}$

Formule di bisezione

$\displaystyle\sin\left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 – \cos(\alpha)}{2}}$

$\displaystyle\cos\left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 + \cos(\alpha)}{2}}$

$\displaystyle\tan\left(\frac{\alpha}{2}\right) = \frac{\sin(\alpha)}{1 + \cos(\alpha)}$

Formule parametriche

$\displaystyle\sin(\alpha) = \frac{2t}{1 + t^2}$

$\displaystyle\cos(\alpha) = \frac{1 – t^2}{1 + t^2}$

$\displaystyle\tan(\alpha) = \frac{2t}{1 – t^2}$

Dove $\displaystyle\tan\left(\frac{\alpha}{2}\right)=t$.

Formule di prostaferesi

$\displaystyle\sin(\alpha) + \sin(\beta) = 2\sin\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha – \beta}{2}\right)$

$\displaystyle\cos(\alpha) + \cos(\beta) = 2\cos\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha – \beta}{2}\right)$

$\displaystyle\sin(\alpha) – \sin(\beta) = 2\cos\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha – \beta}{2}\right)$

$\displaystyle\cos(\alpha) – \cos(\beta) = -2\sin\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha – \beta}{2}\right)$

Formule di Werner

$\displaystyle\sin(\alpha)\sin(\beta) = \frac{1}{2}[\cos(\alpha-\beta) – \cos(\alpha+\beta)]$

$\displaystyle\cos(\alpha)\cos(\beta) = \frac{1}{2}[\cos(\alpha-\beta) + \cos(\alpha+\beta)]$

$\displaystyle\sin(\alpha)\cos(\beta) = \frac{1}{2}[\sin(\alpha+\beta) + \sin(\alpha-\beta)]$